Connaissez-vous vraiment AES ?

AES, ou Advanced Encryption Standard, est l'algorithme de chiffrement symétrique de référence. Mais quels sont les éléments qui l'ont rendu résistants aux attaques depuis plus de 20 ans ?

Il a été établi par le NIST à la suite d'un concours visant à trouver le remplaçant de DES, qui a été craqué à cause d'une limite de taille de clé trop basse. Le gagnant fut la variante de Rindjael, aujourd'hui connu sous l'acronyme AES.

Cet algorithme est composé de 5 mécanismes distincts : Subbytes, Shiftrows, Mixcolumns , Addroundkey et le Key Schedule . Avant de les détailler, quelques connaissance préalable sont nécessaire.

Premièrement, AES travaille dans un corps fini, noté GF(2⁸). Concrètement, cela signifie qu'il travaille avec 2 valeurs (0 et 1) sur 8 éléments , soit un octet. Un corps fini à puissance à besoin d'un modulo, afin de pouvoir rester dans le corps lorsque qu'une opération dépasse la valeur possible sur 1 octet.Le modulo choisi pour AES est x⁸+x⁴+x³+x+1, qui sera référé comme le modulo N par la suite.

AES est un chiffrement par bloc, autrement dit chaque message / fichier chiffré est découpé en bloc de 128 bits, qui sont traités comme une matrice de 4*4 octets.

Les 5 Mécanismes

Subbytes

Subbytes est composé de 2 étapes :

• L'inversion modulaire de chaque octet, signifiant que chaque octet d'entrée A est remplacé par l'octet B qui résout l'équation A*B congru à 1 modulo N
• Une transformation affine A.K.A 5 XOR consécutifs pour chaque bit de chaque octets avec d'autres bits du même octet, et un bit d'un octet fixe

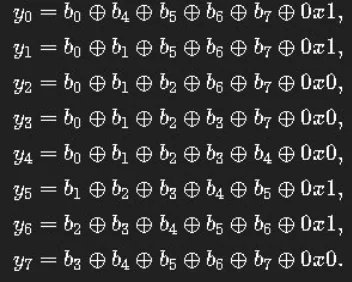
Cette partie introduit la non-linéarité dans AES, c'est à dire l'impossibilité de réduire le chiffrement AES à une équation de faible degré.

Shiftrows

Cette étape consiste simplement à faire une rotation horizontale des lignes de la matrice, avec un décalage e 0 à la première ligne, 1 à la seconde , 2 à la troisième et 3 à la quatrième, comme l'illustre la capture ci dessous:

Mixcolumns

Mixcolumns consiste à prendre chaque colonnes d'éléments (exemple avec la sortie de Shiftrows A1,A6,A11,16) et de les multiplier par une matrice donnée, fixe et connue publiquement. Cette étape, combinée à Shiftrows , permet de faire en sorte que chaque octet de sortie dépende d'un maximum d'octets d'entrée différents, limitant l'apparition de motifs dans des blocs d'entrées similaires.

Addroundkey

Cette étape est l'inclusion de la clé dans l'algorithme, qui permet de s'assurer que seul les possesseurs de cette clé puissent déchiffrer le message. Le résultat des étapes précédentes est XOR avec une sous clé dérivée de la clé principale à travers le key schedule

Key schedule

La clé principale est découpée en "words" noté W de 32 bits, soit 4 pour une clé de 128 bits pour générer des sous-clés de taille fixe de 128 bits. il faut autant de sous clés que de tours, soit 10 pour AES 128 , menant à un total de 40 mots à générer.

Un mot d'indice i est défini par :

ou f est une fonction, dont la définition varie en fonction de la valeur de i modulo nombre de mots de la clé principale, soit 4 pour AES 128.

Ces opérations sont répétées à travers les tours, à l’exception du round "0" (subbytes + addroundkey) et dernier round (Subbytes + Shiftrows + Addroundey) . Cependant, en voyant que l'implication de la clé est tardive dans l'algorithme, on pourrait légitimement se demander : Les étapes intermédiaires sont elles si importantes? C'est ce que nous allons voir avec une implémentation partielle d'AES sans Subbyte.

Vulnérabilité

Dans cette implémentation sans Subbyte, le résultat du tour zéro est :

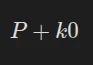
Où P est le texte clair (plain), k0 la clé d'origine et + étant l'équivalent du XOR dans GF(2⁸) au 1 er tour , sans subbytes, le résultat est:

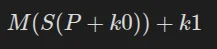
Où M correspond à Mixcolumns , S à Shiftrows et k1 la première sous clé. Cette logique s'applique pour chaque round, sans Mixcolumns pour le 10ème tour

Pour simplifier l'équation finale, nous pouvons établir A = MS , ce qui nous donne: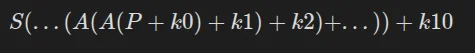

Nous pouvons développer cette équation: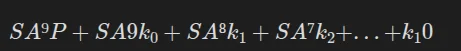

Et là, catastrophe!

On réalise que le texte clair peut être isolé du reste de l'équation: si l'on pose: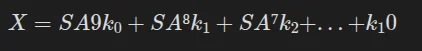 

On peut poser l'équation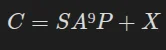 ou C est le texte chiffré. Cela veut aussi dire que :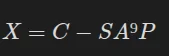

Or SA⁹P n'est PAS dépendant de la clé, signifiant qu'il peut être calculé sans la connaître et X est indépendant du texte clair, signifiant que si nous le calculons une fois nous pouvons récupérer n'importe quel texte à partir du chiffré:

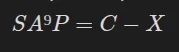
En résolvant "simplement" (cough cough) SA⁹P

Travaux pratiques

Pour ceux étant arrivé jusqu'ici, félicitations. Afin de réaliser notre petite expérience, il nous faut une implémentation d'AES dont les étapes sont modulable. Sous python , la plus connue ne possède pas cette flexibilité. Après divers tentatives de création manuelle ,(Règle un de la cryptographie : ne jamais implémenter ses propres algorithmes).

J'ai découvert ne pas être le premier à m'être penché sur le sujet, et qu'une implémentation existait correspondant à mes besoins déjà sur Github: https://github.com/bozhu/AES-Python/blob/master/aes.py

Le POC suivant est la démonstration complète de la vulnérabilité, qui permet de déchiffrer n'importe quel texte à partir d'un paire texte clair / sortie chiffrée connue. Il suffit de l'exécuter dans le même dossier que le fichier aes.py mentionné ci dessus pour l'exécuter:

#!/usr/bin/env python3
# SubAES.py - Démonstration combinant AES (Bo Zhu) et algèbre linéaire sur GF(2)

import os
import numpy as np
from aes import AES

# ============================================================
# ---------- CONVERSIONS BYTES <-> MATRICES DE BITS ----------
# ============================================================

# Force les matrice à rester dans GF(2)
def gf2(a):
    return (np.asarray(a, dtype=np.uint8) & 1)
    
# Multiplication matricielle dans GF(2)
def gf2_dot(A, B):
    return gf2((A.astype(np.uint8) @ B.astype(np.uint8)) % 2)

# Addition dans GF(2) A.K.A XOR
def gf2_add(A, B):
    return gf2((A.astype(np.uint8) + B.astype(np.uint8)) % 2)

#crée une matrice d'identité de taille n ( équivalent de fois 1 mais pour les matrices)
def gf2_eye(n):
    return gf2(np.identity(n, dtype=np.uint8))

#combine des matrices en une seule
def block_matrix(blocks):
    rows = [np.hstack(row) for row in blocks]
    return gf2(np.vstack(rows))

# Calcule la matrice A puissance e dans GF(2)
def gf2_mat_pow(A, e):
    assert A.shape[0] == A.shape[1]
    n = A.shape[0]
    result = gf2_eye(n)
    base = A.copy()
    while e > 0:
        if e & 1:
            result = gf2_dot(result, base)
        base = gf2_dot(base, base)
        e >>= 1
    return result

# Calcule l'inverse d'une matrice carrée dans GF(2) en utilisant l'élimination de Gauss mod 2
def gf2_mat_inv(A):
    A = gf2(A.copy())
    n = A.shape[0]
    assert A.shape[0] == A.shape[1]
    aug = np.hstack([A.astype(np.uint8), gf2_eye(n).astype(np.uint8)])
    row = 0
    for col in range(n):
        pivot = None
        for r in range(row, n):
            if aug[r, col] == 1:
                pivot = r
                break
        if pivot is None:
            raise np.linalg.LinAlgError("Matrix is singular in GF(2)")
        if pivot != row:
            aug[[pivot, row]] = aug[[row, pivot]]
        for r in range(n):
            if r != row and aug[r, col] == 1:
                aug[r, :] ^= aug[row, :]
        row += 1
        if row == n:
            break
    inv = aug[:, n:]
    return gf2(inv)

# ============================================================
# ---------- CONVERSIONS BYTES <-> MATRICES DE BITS ----------
# ============================================================

def bytes2mat(b):
    """16 bytes -> 1 x 128 row-vector (np.uint8) of bits  Example: b'AB' -> [0,1,0,0,0,0,0,1, 0,1,0,0,0,0,1,0]"""
    if not isinstance(b, (bytes, bytearray)):
        raise TypeError("bytes2mat expects bytes input")
    bits = []
    for i in b:
        tmp = format(i, "08b")
        bits.extend(int(ch) for ch in tmp)
    arr = np.array(bits, dtype=np.uint8).reshape(1, -1)  # shape (1,128)
    return gf2(arr)

def mat2bytes(m):
    """
    Convert 1x128 or 128x1 bit matrix -> 16-byte value.
    Reverse of bytes2mat.
    """
    m = np.asarray(m, dtype=np.uint8)
    if m.shape == (128, 1):
        row = m[:, 0]
    elif m.shape == (1, 128):
        row = m[0, :]
    else:
        row = m.flatten()
        if row.size != 128:
            raise ValueError("matrix must represent 128 bits")
    bits = ''.join(str(int(x)) for x in row)
    bytes_list = [int(bits[i:i+8], 2) for i in range(0, 128, 8)]
    return bytes(bytes_list)


# ============================================================
# ---------- CONSTRUCTION DES MATRICES (SIMULE AES) ----------
# ============================================================
I = gf2_eye(8)
X = gf2(np.zeros((8, 8), dtype=np.uint8))
for i in range(7):
    X[i, i+1] = 1

X[3, 0] = 1

X[4, 0] = 1

X[6, 0] = 1

X[7, 0] = 1

# Combiner les blocs pour former une matrice  32*32 (simule Mixcolumns)
C = block_matrix([
    [X, gf2_add(X, I), I, I],
    [I, X, gf2_add(X, I), I],
    [I, I, X, gf2_add(X, I)],
    [gf2_add(X, I), I, I, X]
])

# Création de matrice "zéro" pour construire les grandes matrices
zeros = gf2(np.zeros((8, 8), dtype=np.uint8))
zeros2 = gf2(np.zeros((32, 32), dtype=np.uint8))

# Matrices "de sélection" pour créer une permutation cyclique S
o0 = block_matrix([
    [I, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros]
])

o1 = block_matrix([
    [zeros, zeros, zeros, zeros],
    [zeros, I, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros]
])

o2 = block_matrix([
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, I, zeros],
    [zeros, zeros, zeros, zeros]
])

o3 = block_matrix([
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, zeros],
    [zeros, zeros, zeros, I]
])
#Matrice de permutation S (fait tourner les 4 blocs de manière cyclique)
S = block_matrix([
    [o0, o1, o2, o3],
    [o3, o0, o1, o2],
    [o2, o3, o0, o1],
    [o1, o2, o3, o0]
])

\
M = block_matrix([
    [C, zeros2, zeros2, zeros2],
    [zeros2, C, zeros2, zeros2],
    [zeros2, zeros2, C, zeros2],
    [zeros2, zeros2, zeros2, C]
])

# Combine les matrices pour former une transformation linéaire de 128x128
R = gf2_dot(M, S) #Tour 1
R9 = gf2_mat_pow(R, 9) #Tour consécutifs
A = gf2_dot(S, R9) # Dernier tour donnant SA⁹ 

# ---------------------------
# AES sans SubBytes (linéarisation)
# ---------------------------
do_nothing = lambda *x: None

# Crée une instance d’AES avec une clé aléatoire (en entier, contrainte de l'impémentation AZS de Bo Zhu)
key_int = int.from_bytes(os.urandom(16), byteorder="big")
c = AES(key_int)

#nullifie l'étape Subbyte
setattr(c, "_AES__sub_bytes", lambda s: None)

# Prépare deux textes clairs de 16 octets

p_bytes = b"Very secret text"       # 16 octets secrest

p_int = int.from_bytes(p_bytes, "big")
ct_int = c.encrypt(p_int)
ct_bytes = ct_int.to_bytes(16, "big")

p2_bytes = b"Known plaintextt"      # texte clair connu (pour l’attaque)
p2_int = int.from_bytes(p2_bytes, "big")
ct2_int = c.encrypt(p2_int)
ct2_bytes = ct2_int.to_bytes(16, "big")

# ============================================================
# ---------- ATTAQUE LINÉAIRE : RÉCUPÉRATION DU TEXTE --------
# ============================================================

# Conversion des textes en vecteurs de bits (colonnes de 128 bits)
p2_row = bytes2mat(p2_bytes)   # 1 x 128
p2_col = p2_row.T              # 128 x 1

ct2_row = bytes2mat(ct2_bytes)
ct2_col = ct2_row.T

# Calcule le vecteur constant X = ct2 - A*p2  (sur GF(2), la soustraction = addition)
A_p2 = gf2_dot(A, p2_col)         # 128 x 1
X = gf2_add(ct2_col, A_p2)        # 128 x 1

# Récupération du texte inconnu : p = A⁻¹ * (ct - K)
ct_col = bytes2mat(ct_bytes).T    # 128 x 1

inner = gf2_add(ct_col, X)        # ct - X

Ainv = gf2_mat_inv(A)
res_col = gf2_dot(Ainv, inner)    # 128 x 1

res_row = res_col.T                # 1 x 128

recovered_plaintext = mat2bytes(res_row)
	
print("original plaintext  :", p_bytes)
print("recovered plaintext :", recovered_plaintext)
print("match:", recovered_plaintext == p_bytes)

Au delà de la sortie assez sommaire , le cœur de la logique est ici:

R = gf2_dot(M, S) #Tour 1
R9 = gf2_mat_pow(R, 9) #Tour consécutifs
A = gf2_dot(S, R9) # Dernier tour donnant SA⁹ 

p2_row = bytes2mat(p2_bytes)   # 1 x 128
p2_col = p2_row.T              # 128 x 1

ct2_row = bytes2mat(ct2_bytes)
ct2_col = ct2_row.T

A_p2 = gf2_dot(A, p2_col)        
X = gf2_add(ct2_col, A_p2) 

"A" Dans la démonstration correspond à SA⁹ et p2_col au texte clair P connu . En soustrayant a la valeur du texte chiffré cette somme, on obtient X, la partie constante générée par l'introduction d'Addroundkey. Une fois cette valeur acquise, il suffit de prendre le chiffré d'un texte secret et d'y soustraire X pour trouver SA⁹P_secret

ct_col = bytes2mat(ct_bytes).T    # 128 x 1
inner = gf2_add(ct_col, X)        # ct - X

Il suffit ensuite de multiplier le résultat par l'inverse de A (=SA⁹) pour n'avoir plus que le texte secret en clair.

Ainv = gf2_mat_inv(A) 
res_col = gf2_dot(Ainv, inner)    # multiplication par l'inverse de A, récupérant la valeur du texte secret en clair
res_row = res_col.T                
recovered_plaintext = mat2bytes(res_row)

Ce POC est limité à un flag de 16 caractères exactement, n'ayant implémenté ni padding ni gestion de multiple bloc, mais la logique d'exploitation resterait la même. avec la même valeur de X par défaut .